: How to Find Horizontal Asymptotes:

Introduction

When analyzing the behavior of functions, especially rational functions, it’s crucial to understand the concept of horizontal asymptotes. These asymptotes give us a clear picture of how a function behaves as $x$ approaches infinity or negative infinity. In this article, we will explore how to find horizontal asymptotes for different types of functions, the rules governing horizontal asymptotes, and some practical examples to guide your understanding. Additionally, we’ll address some frequently asked questions (FAQs) related to horizontal asymptotes.

What Are Horizontal Asymptotes?

A horizontal asymptote is a line that a function approaches as $x$ tends towards positive or negative infinity. For a function $f(x)$, if the graph of $f(x)$ approaches a constant value $y=c$ as $x\to \infty$ or $x\to -\infty$, then $y=c$ is a horizontal asymptote.

Horizontal asymptotes provide insight into the long-term behavior of a function, helping us understand how the function behaves at extreme values of $x$.

How to Find Horizontal Asymptotes for Rational Functions

The most common scenario where you need to find horizontal asymptotes is when dealing with rational functions, which are functions that are the ratio of two polynomials. A rational function has the general form:

f(x)=P(x)Q(x)f(x) = \frac{P(x)}{Q(x)}f(x)=Q(x)P(x)​

Where $P(x)$ and $Q(x)$ are polynomials. The rules for determining horizontal asymptotes depend on the degrees of the polynomials $P(x)$ and $Q(x)$.

Step-by-Step Process:

To find horizontal asymptotes for a rational function, follow these steps:

1. Identify the degrees of the polynomials:

   • Let the degree of $P(x)$ be $m$.
   • Let the degree of $Q(x)$ be $n$.

2. Compare the degrees of the polynomials:

   • Case 1: $m<n$
     If the degree of the numerator is less than the degree of the denominator, the horizontal asymptote is $y=0$. This means that as $x\to \infty$ or $x\to -\infty$, the function gets closer and closer to 0.

   • Case 2: $m=n$
     If the degrees of the numerator and the denominator are equal, the horizontal asymptote is found by dividing the leading coefficients of the numerator and denominator. Specifically, if the leading coefficient of $P(x)$ is $a$ and the leading coefficient of $Q(x)$ is $b$, then the horizontal asymptote is y=aby = \frac{a}{b}y=ba​.

   • Case 3: $m>n$
     If the degree of the numerator is greater than the degree of the denominator, there is no horizontal asymptote. However, there may be an oblique asymptote instead, which requires a different method to find.

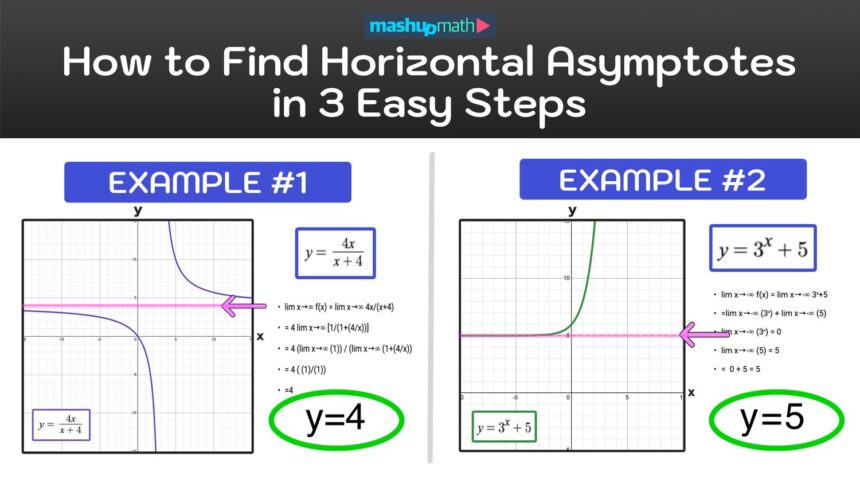
Example 1: Finding Horizontal Asymptotes

Let’s consider the following rational function:

f(x)=3×2+5x+2×2+4f(x) = \frac{3x^2 + 5x + 2}{x^2 + 4}f(x)=x2+43x2+5x+2​

Here, the degree of the numerator ($m=2$) is equal to the degree of the denominator ($n=2$).

According to Case 2, we divide the leading coefficients. The leading coefficient of the numerator is 3, and the leading coefficient of the denominator is 1. Thus, the horizontal asymptote is:

y=31=3y = \frac{3}{1} = 3y=13​=3

So, the horizontal asymptote for this function is $y=3$.

Example 2: Horizontal Asymptotes of a Different Function

Now, let’s consider the rational function:

f(x)=2xx3+3x+1f(x) = \frac{2x}{x^3 + 3x + 1}f(x)=x3+3x+12x​

Here, the degree of the numerator ($m=1$) is less than the degree of the denominator ($n=3$).

According to Case 1, the horizontal asymptote is $y=0$. As $x$ approaches infinity or negative infinity, the function will approach 0.

Why Are Horizontal Asymptotes Important?

Understanding how to find horizontal asymptotes is essential for several reasons:

1. Long-Term Behavior: Horizontal asymptotes tell us how the function behaves for very large or small values of $x$. This can be critical in fields like physics or economics, where understanding the behavior at extremes is important.

2. Graphing Functions: When sketching the graph of a rational function, horizontal asymptotes give you a guideline for the behavior of the function at both ends of the graph.

3. Calculus Applications: Horizontal asymptotes are related to limits in calculus. Knowing how to find them helps with solving limit problems, particularly when approaching infinity.

Common Pitfalls When Finding Horizontal Asymptotes

When finding horizontal asymptotes, students often make the following mistakes:

1. Incorrectly assuming a horizontal asymptote exists when it doesn’t: Remember, if the degree of the numerator is greater than the degree of the denominator, no horizontal asymptote exists, although an oblique asymptote might.

2. Forgetting to compare degrees properly: Always compare the degrees of the numerator and the denominator. If the degrees are equal, divide the leading coefficients, not the full polynomials.

FAQs on Horizontal Asymptotes

1. What is the difference between horizontal and vertical asymptotes?

   • Horizontal asymptotes describe the behavior of a function as $x\to \infty$ or $x\to -\infty$, while vertical asymptotes describe the behavior as $x$ approaches a specific finite value. Vertical asymptotes typically occur when the denominator of a rational function is zero.

2. Can a function have more than one horizontal asymptote?

   • No, a function can have at most one horizontal asymptote because the horizontal asymptote represents the behavior of the function at both ends of the graph (as $x\to \infty$ and $x\to -\infty$).

3. Does a function always approach the horizontal asymptote?

   • Not necessarily. While the function will approach the horizontal asymptote as $x\to \infty$ or $x\to -\infty$, it may never reach it, depending on the nature of the function. The asymptote simply represents the value the function is approaching.

4. Do horizontal asymptotes exist for all functions?

   • No, horizontal asymptotes only exist for rational functions or other functions where the output tends toward a constant as $x\to \infty$ or $x\to -\infty$. Functions like polynomials or exponential functions may not have horizontal asymptotes.

5. What happens if the degree of the numerator is greater than the denominator?

   • If the degree of the numerator is greater than the degree of the denominator, the function does not have a horizontal asymptote. Instead, there may be an oblique (slant) asymptote.

Conclusion

In this article, we’ve covered everything you need to know about how to find horizontal asymptotes. Understanding the rules based on the degrees of the polynomials involved is the key to determining these asymptotes. Whether the degrees of the numerator and denominator are equal, or the degree of the numerator is less than or greater than the denominator, knowing the appropriate case will guide you to the correct horizontal asymptote. By practicing with examples and applying these principles, you will gain confidence in analyzing the behavior of rational functions.

Summary

To summarize, here’s a brief recap of how to find horizontal asymptotes for rational functions:

• Degree of numerator < degree of denominator: Horizontal asymptote at $y=0$.
• Degree of numerator = degree of denominator: Horizontal asymptote at y=leading coefficient of numeratorleading coefficient of denominatory = \frac{\text{leading coefficient of numerator}}{\text{leading coefficient of denominator}}y=leading coefficient of denominatorleading coefficient of numerator​.
• Degree of numerator > degree of denominator: No horizontal asymptote (look for oblique asymptotes).

With this knowledge, you can confidently approach horizontal asymptotes in calculus and other mathematical studies.