It all started on a quiet Sunday afternoon. Jamie, a high school student, was helping her mother redesign their garden. Her mom pointed to a triangular flower bed and said, “We need to figure out how much soil we’ll need for this area.” Jamie froze. She’d just covered this in school but still wasn’t sure she knew how to find the area of a triangle.
Like Jamie, many of us learned formulas in school but didn’t always see how they apply in real life. Yet knowing how to find the area of a triangle isn’t just about passing a math test. It’s a useful life skill—whether you’re measuring land, sewing fabric, or doing home improvement projects.
In this article, we’ll walk through several methods to calculate the area of a triangle using real-life examples, simple words, and clear steps.
Why Knowing How to Find the Area of a Triangle is Helpful
You don’t have to be an engineer or architect to benefit from this knowledge. Triangles appear in everything from art and design to construction and gardening. Knowing how to find the area of a triangle helps you calculate space accurately, saving both time and materials.
Let’s say you’re laying tiles in a corner of a room or designing a triangular shelf. If you know the base and height of the triangle, you can quickly calculate how much material you need. It’s practical math—no complicated equations needed.
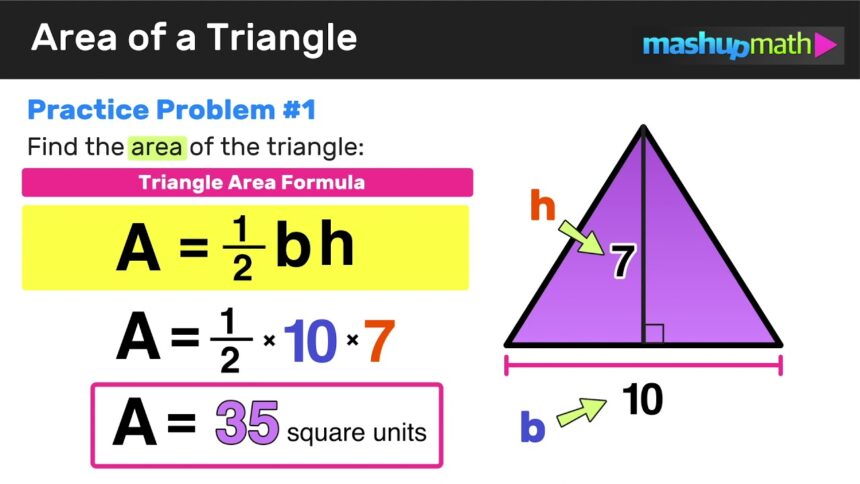
The Most Common Formula: Base × Height ÷ 2
The easiest and most commonly used method is:
Area = ½ × base × height
-
The base can be any one side of the triangle.
-
The height is the perpendicular distance from the opposite corner to that base.
Example:
Let’s say your triangle has a base of 12 cm and a height of 8 cm.
Area = ½ × 12 × 8 = 48 cm²
This method is fast and works perfectly when the height is known or can be easily measured.
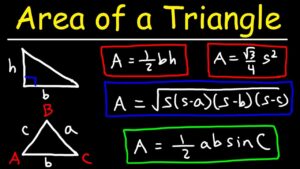
What If You Don’t Know the Height? Try Heron’s Formula
Jamie didn’t have a ruler long enough to measure the flower bed’s height. Instead, she measured all three sides: 7 feet, 9 feet, and 10 feet. In cases like this, Heron’s Formula comes in handy.
Steps:
-
Calculate the semi-perimeter:
s = (a + b + c) ÷ 2s = (7 + 9 + 10) ÷ 2 = 13
-
Plug into Heron’s Formula:
Area = √[s(s − a)(s − b)(s − c)]
Area = √[13(13 − 7)(13 − 9)(13 − 10)]
Area = √[13 × 6 × 4 × 3]
Area = √936 ≈ 30.6 ft²
Heron’s Formula is especially helpful when the triangle is irregular and doesn’t have an easy-to-measure height.
How to Find the Area of a Triangle Using Angles and Sides
Sometimes, you’re given two sides and the angle between them. There’s a formula for that too:
Area = ½ × a × b × sin(C)
Where:
-
a and b are sides of the triangle
-
C is the included angle
Example:
Suppose side A is 6 cm, side B is 10 cm, and the angle between them is 45°.
Area = ½ × 6 × 10 × sin(45)
Area = 30 × 0.7071 ≈ 21.2 cm²
This method uses trigonometry but works well for non-right triangles where angles are provided.
Using a Right Triangle? It’s Even Easier
In a right triangle, the two sides that meet at the right angle act as the base and height.
Example:
If one side is 5 m and the other is 12 m:
Area = ½ × 5 × 12 = 30 m²
No need for additional steps, just plug in the numbers.
Real-Life Story: Building a Treehouse
A few months after the garden project, Jamie’s father asked her to help build a treehouse platform. The support beams formed triangles underneath. Jamie measured the base and the height of each triangular frame, calculated the area using the simple formula, and figured out how much wood they’d need. Her math skills saved money and helped complete the project faster.
What once seemed like a random math lesson in class had become a real-world problem she could solve confidently.
Tips for Calculating Triangle Area
-
Draw a sketch of the triangle to understand the dimensions.
-
Label the sides and angles clearly.
-
Always use the same units (cm, m, inches, etc.) for all measurements.
-
For height, remember it must be perpendicular to the base.
Common Mistakes to Avoid
-
Using the wrong height – It has to be perpendicular, not just any side.
-
Forgetting to divide by 2 in the base × height formula.
-
Incorrect angle units – Make sure your calculator is in the right mode (degrees vs. radians).
-
Mismatched units – Mixing inches and centimeters can mess up your answer.
Double-checking your work can help avoid simple errors.
Final Thoughts
Learning how to find the area of a triangle isn’t just about math class—it’s about understanding a concept you can use throughout life. Whether you’re solving homework, building something, or even crafting, triangles show up more often than you’d think.
With just a few key formulas—like ½ × base × height or Heron’s Formula—you’ll be able to calculate the area of any triangle with ease. Even if math wasn’t your favorite subject, this is one skill that’s well worth mastering.
Meta Description:
Learn how to find the area of a triangle using easy-to-follow formulas and examples. Discover simple methods anyone can use, even without advanced math skills.